Strongly-coupled plasmas and warm dense matter
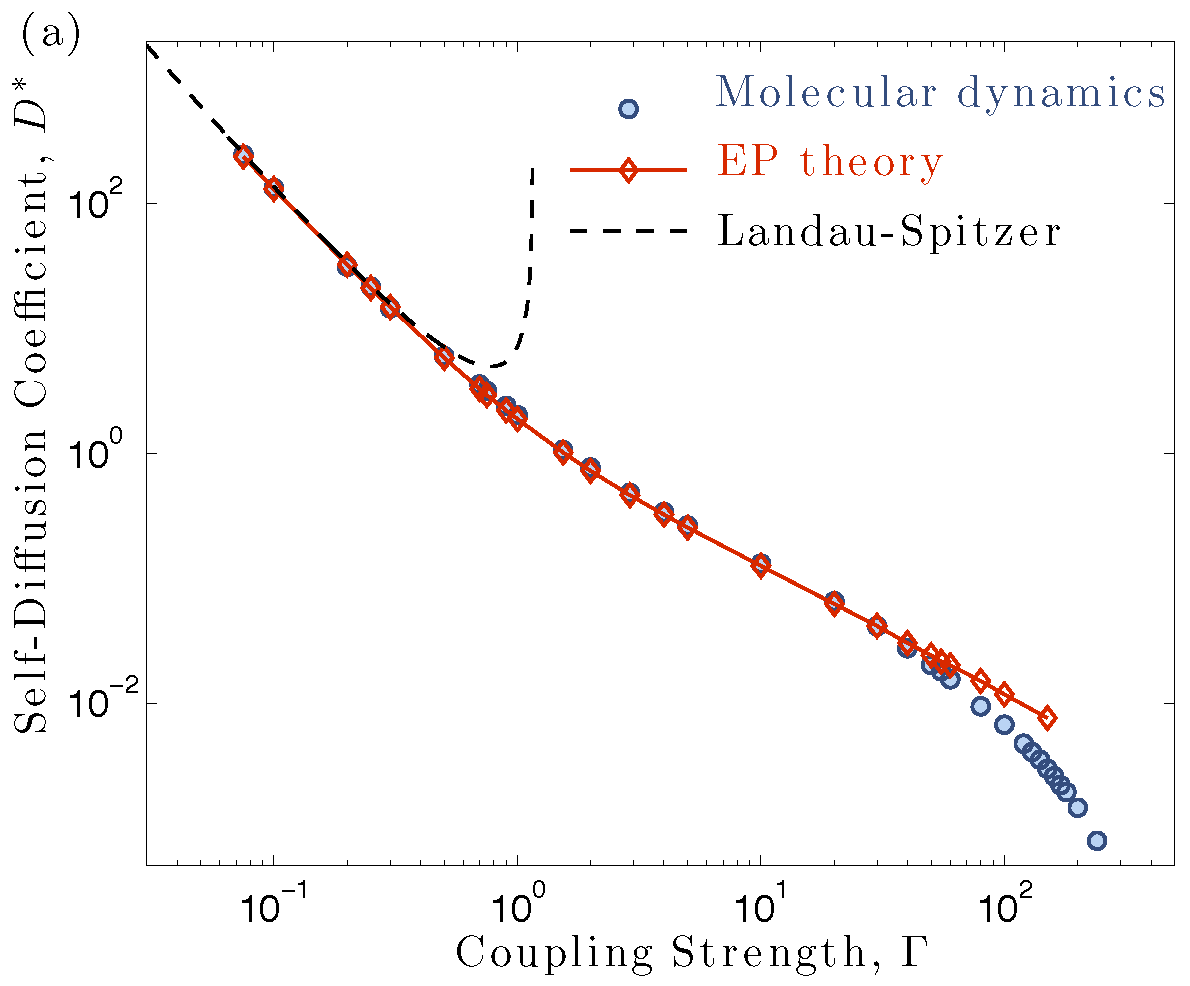
These figures show predictions of the effective potential theory (EPT) from [S2,S4,S6] for self-diffusion (left) and shear viscosity (right) of the one-component plasma. Traditional plasma theory (dashed lines) breaks down when the coupling strength approaches 1. EPT is capable of extending plasma theory well into the strongly coupled regime. Circles show results of molecular dynamics simulations, which provide an accurate (though computationally expensive) solution for these transport properties.
In traditional weakly coupled plasmas, the kinetic energy of individual particles greatly exceeds the potential energy of their interaction. Strongly coupled plasmas occur in the opposite limit. Strong coupling can be achieved in three ways:
(1) High ion charge numbers, as found in dusty plasmas
(2) High density, as found in inertial confinement fusion as well as dense astrophysical objects such as white dwarf stars, neutron star crusts and giant planet interiors
(3) Low temperature, as found in non-neutral plasmas, ultracold neutral plasmas and antimatter plasmas.
In addition, electrons in the dense plasma examples are typically described by quantum statistics, rather than the classical statistics found in conventional plasmas. The regime where ions are strongly coupled and electrons are quantum degenerate is often called warm dense matter. The fundamental physical properties of warm dense matter are substantially different than others (liquid, gas, plasma or solid) that it may be considered a different state of matter.
In our group, we develop theories intended to provide a predictive description of various fundamental processes in these exotic plasma states. A major focus is to develop theoretical models for transport properties, such as electrical resistivity, thermal conductivity, viscosity, etc., that can be evaluated efficiently enough to be implemented in the large hydrodynamics simulations that are used to simulate macroscopic behavior of the experiments and astrophysical objects. A typical research program consists of first developing an approximate transport theory using methods from plasma kinetic theory, liquid theory, and statistical mechanics. The second stage is a verification procedure, where the theory is tested against predictions of ab inito particle simulations, which is usually some form of molecular dynamics simulation. When data is available, the theory is tested against experiments. Finally, verified transport coefficients are implemented in various hydrodynamics simulations, and the influence of coupling and/or quantum effects on macroscopic behavior of the experimentally-relevant plasma can be quantified.
Applications
The primary application of this work is fusion energy research. Specifically, plasmas in inertial confinement fusion (ICF) experiments evolve through an enormous range of density and temperature, including the warm dense matter regime. Our work is motivated, in part, by the need for more accurate descriptions of the materials properties at these conditions in order to model the evolution of the plasma in ICF experiments. There are several other related applications, including modeling of dense astrophysical objects (such as white dwarfs and the interior of giant planets), dense plasmas created by the interaction of intense lasers with matter, dusty plasmas, ultracold plasmas, and nonneutral plasmas. Part of the excitement of basic physics research is that new physics discoveries often lead to new applications!
Links
Theory:
Los Alamos Dense Plasma Theory: Daligault’s Group (our primary collaborator)
Michael Bonitz’s Group
Warm Dense Matter:
Matter in Extreme Conditions at SLAC
Ultracold Neutral Plasmas:
Ultracold Atoms and Plasmas: Killian’s Group
U. Maryland: Rolston Group
Colorado State: Roberts Group
Auburn: Robicheaux Group
Brigham Young University: Bergeson Group
Nonneutral Plasmas:
UCSD Nonneutral Plasma Group
Strongly Coupled Dusty Plasmas:
Goree Dusty Plasma Group
Cavitation/Sonoluminescence:
UCLA: Putterman Group